开关电源变压器铁芯气隙的选取

前面已经提过，单击式开关电源变压器由于输入电压为单极性电压脉冲，当脉冲幅度和宽度超过变压器的伏秒容量时，变压器铁芯将出现磁饱和。为了防止开关变压器铁芯出现磁饱和最简单的方法是在变压器铁芯中留气隙，或采用反磁场。

当在变压器铁芯中留有气隙时，由于空气的导磁率只有铁芯导磁率的几千分之一，磁动势几乎都降在气隙上面;因此，留有气隙的变压器铁芯，其平均导磁率将会大大下降;不但剩余磁通密度也会降低，而且最大磁通密度Bm可以达到饱和磁通密度Bs;从而使磁通增量增大，变压器铁芯不再容易出现磁饱和。如图2-24所示是留有气隙的变压器铁芯的工作原理图与磁化曲线图 。

在图2-24-a中，假设l1 为气隙长度，变压器铁芯磁路的总长度为 lc，则磁路的磁通势为：

△Hlc=△B(l1-lc)/μc +△Bl1/μ0

上式中， μc为变压器铁芯的导磁率; μ0为空气的导磁率，其值约等于1; lc为变压器铁芯磁路的总长度; l1为气隙的长度; △H为磁场强度增量; △B为磁通密度增量。

由于 lc >>l1 ，μ0≈1 ，所以，( lc-l1 )≈lc ，因此上式可化简为：

上式中， μa为有气隙铁芯的平均导磁率， μc为变压器铁芯的导磁率， l1为气隙的长度， lc为变压器铁芯磁路的总长度。

(2-72)式中，由于μc 不是一个常数，我们不能用求导数的方法把 l1当成一个变数来求 μa的最大值;另外，求 μa的最大值也不是我们的主要目的;我们的愿望是在最大磁通密度增量 △B 的条件下，要求平均导磁率 μa也能达到最大。

我们再来看图2-24-b。在图2-24-b中，虚线表示变压器铁芯没有气隙时的磁滞回线，实线表示变压器铁芯留有气隙时的磁滞回线，其中磁化曲线o-a为留有气隙铁芯的基本磁化曲线。这里的基本磁化曲线与初始磁化曲线并不完全相同，这里的基本磁化曲线相当于磁化曲线的几何平均值，以便用于分析磁场强度增量 △H 与磁感应密度增量 △B 的关系。

显然，对应每一个气隙长度的取值就有一组相应的磁滞回线;但不管气隙长度取得多大，铁芯的最大磁通密度Bm只能达到铁芯磁饱和时对应的Bs值，它不会随着气隙长度l1 的增长而继续增长;而铁芯的剩余磁通密度Br也不会因气隙长度l1增长而大幅度下降。因此， l1应该有一个最佳值，它应该既要兼顾磁通密度增量 △B的最大，也要兼顾平均导磁率μa 达到最大的条件。

为了求出 的最佳值，我们可以沿着基本磁化曲线o-a不断地画切线，如图中切线o-b;切线与H轴夹角β 的正切值tgβ 就是此点的导磁率;当切线的相切点位于最大磁通密度增量△B 的二分之一位置上时，这点的正切值tgβ 就可以认为等于平均导磁率μa ;由此我们可以看出平均导磁率μa 总是小于或者等于正切值 tgβ 。

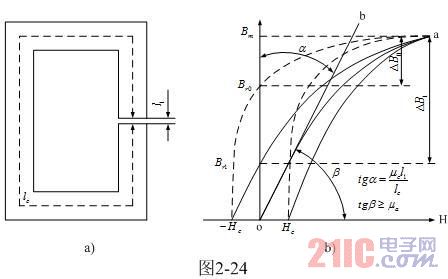
如果我们把最大正切值tgβ 对应的磁通密度增量△B 和磁场强度增量△H ，定义为铁芯的最佳工作点，那么通过切线o-b就可以求出对应的l1最佳值。可以证明通过原点的切线o-b是正切值最大的切线，因为实际中的基本磁化曲线是不存在的，基本磁化曲线相当于磁化曲线的几何平均值，是一条按电容充电规律变化的指数曲线(请参考《2-1-1-9.开关电源变压器铁芯磁滞回线测量》章节的内容);另外，所定义的最佳工作点就是气隙长度l1 最小值对应的工作点。

从图2-24-b以及(2-72)式可以看出，当 μcl1/lc>>1时，有气隙铁芯的平均导磁率μa 基本与气隙l1 的长度成反比;因此μcl1/lc 的值正好就是对应图2-24-b中，切线o-b与B轴夹角α 的正切值tgα ; △H代表μcl1 ，△B 代表lc。 μc与l1相乘正好把两条正交直线H和B的单位进行归一化，要么它们之间的夹角就没有意义。

由图2-24-b可以看出，当 tgα≈1/2时， l1为最佳值，实际上也是l1 的最小值;因为，平均导磁率μa 会随着 l1增大而减小。因此， l1的最佳值(或最小值)由下式求得：

l1/lc≈2/μc (2-73)