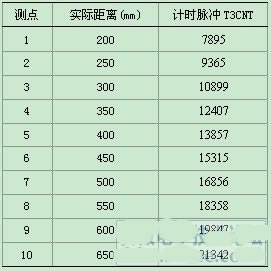
从表中数据可以看出，实际距离每1毫米的变化，计数脉冲有约30个的变化，每个记数脉冲为0.1μs。

3.2 系统响应的实时性

系统每测控一个循环的耗时主要由两部分构成，即超声波对阻尼器的运行状态辩识的时间和电流驱动器接收到控制信号至输出电流稳定的时间，前者由于采用了测量三次通过一定处理后，作为最终的计数脉冲值，每次测量最大耗时约2.5ms，共7.5ms;图6是电流驱动器在阶跃上升和下降信号作用下的实测动态响应图，图中上面是阶跃输入信号曲线，纵向每格的幅值为2.00V;下面是在取样电阻两端实测的响应曲线，纵向每格的幅值为1.00V;横向为时间轴，每格的宽度为2.00ms;可以看出，在阶跃信号激励下，实际的上升时间和下降时间都低于2.5ms，因此系统总的动态响应时间约10 ms，完全满足实时性要求。

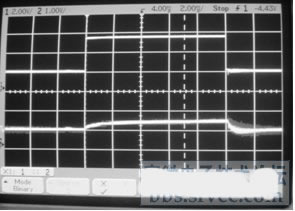
                  图6 电流驱动器的动态响应图

3.3 系统的稳定性

系统的稳定主要由取决于超速波传感和电流驱动器部分，前者由于环境因素的影响可能产生误触发，因此在一个测控循环中，通过对连续三次测量数据结合阻尼器的安装位置和可能运行的最大速度等进行数据有效性分析，从而确定本次循环的准确时间，表2是在同一距离处，静态测量9次的测试结果：

表 2

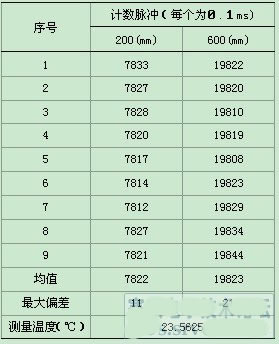
由于阻尼器的电感约2.45mH,静态电阻约1.2?,电流驱动器采用BUCK变换拓扑电路结构时，后面不接平波电感和滤波电容输出的电流纹波已经很小，因此开关管后面的线性部分是典型的一阶惯性环节，通过PI调节后，其单位阶跃响应没有稳态误差，不存在超调量和峰值时间，只要反馈系数取得合适系统都是稳定的。

4、结论

本文采用超声波传感器结合数字信号处理器对磁流变液阻尼器运行状态进行感知，利用脉宽调制(PWM)原理结合磁流变液阻尼器的阻抗特性，设计了其电流源驱动器;软、硬件设计简单、方便，又能满足了系统的实时性和分辨率要求，对类似非接触式动态位移测量系统也有一定的参考价值。

参考文献

[1] K. J. Kitching, D. J. Cole, and D. Cebon. The development of a heavy vehicle semi-active damper[J]. Proc. Intl.Symposium on Advanced Vehicle Control. AVEC’96, Aachen, German, 1996.

[2] Y. He and J. McPhee. A Design Methodology for Mechatronic Vehicles: Application of Multidisciplinary Optimization, Multibody Dynamics, and Genetic Algorithms[J]. submitted to Vehicle System Dynamics, 2004.

[3] Sung-Ryong Hong, Seung-Bok Choi. Vibration Control of a Structural System Using Magneto-Rheological Fluid Mount[J]. Journal of Intelligent Material Systems and Structures, Vol. 16(111-12), 2005.